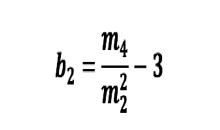Um momento de ordem k centrado em A é dado por:

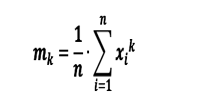
Os momentos empíricos são utilizados para o cálculo das principais medidas estatística.

Classificam-se as medidas descritivas como: - Medidas posição (tendência central e separatrizes)
- Medidas de dispersão
- Medidas de assimetria e de curtose.

Os quartis são percentis 25% (primeiro quartil), 50% (segundo quartil) e 75% (terceiro quartil). Os quartis permitem separar a amostra ordenada em quatro blocos com igual ou quase igual) número de elementos e a sua comparação permite inferir sobre a(as) simetria(s) da amostra. São elas:

Como exemplo vamos calcular o primeiro e o terceiro quartil para a amostra dada. Temos que np = 0,25x22 = 5,5 np = 0,75x22 = 6. Então para o cálculo dos quartis, a fórmula a ser utiliza é para np não inteiro.

A amplitude interquartis é a medida, aproximada, dos 50% valores centrais da amostra. É uma indicação de escala cada vez mais usada.

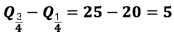
As medidas de posição central são assim denominadas por indicarem um ponto em torno do qual se concentram os dados, dividindo-os em partes iguais. São elas:
- Média
- Mediana
- Moda

A média é uma medida de localização do centro da distribuição dos dados:

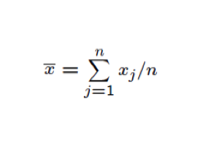
A mediana é um número de um grupo de dados ordenados que separa a metade inferior da amostra, população ou distribuição de probabilidade, da metade superior.

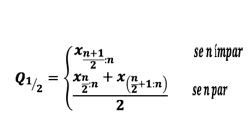
Vamos entender esta fórmula:

Para encontrarmos a mediana, precisamos ordenar os dados e identificar se o tamanho da amostra é par ou ímpar. Como n = 22, é par, logo a mediana é:

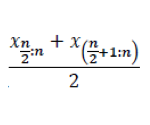
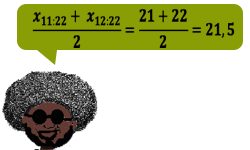
As medidas de dispersão auxiliam as medidas de tendência central a descrever o conjunto de dados adequadamente. São valores positivos e indicam se os dados estão, ou não, próximos uns dos outros. São eles:
- Variância amostral
- Desvio Padrão
- Amplitude Amostral
- Coeficiente de Dispersão
- Coeficiente de Variação

A variância amostral é uma medida de dispersão em relação a média. Quando mais frequentes forem os valores pouco afastados da média estarão, e consequentemente menor dispersão (em relação a média) apresentará a variável aleatória.

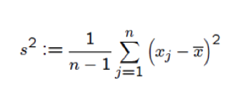
Exemplo utilizando os mesmos dados ordenados:

O desvio padrão é a raiz quadrada da variância amostral:

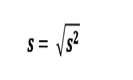
Exemplo utilizando os mesmos dados ordenados:

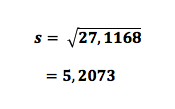
A amplitude é um indicador da dispersão, mas pouco revelador uma vez que 2 amostras podem ter a mesma dispersão e uma ser evidentimente mais dispersa que a outra. É dada por:

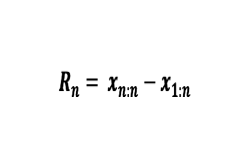
Com os mesmos dados ordenados:

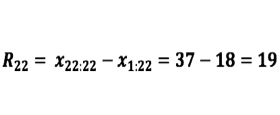
O coeficiente de dispersão é a relação entre o desvio padrão e a média e indica o quão “pesada” é a dispersão para o conjunto de dados. É dada por s/x_

O coeficiente de variação é a característica amostral de dispersão que relativiza o desvio padrão em termos da média. Este coeficientes só se emprega quando a variável toma valores de um só sinal, e é dada por:

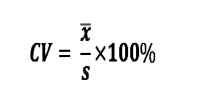
Com os mesmos dados ordenados:

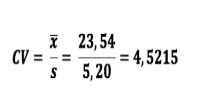
Com os mesmos dados ordenados:

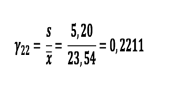
O coeficiente de assimetria empírico dá-nos indicações sobre o peso relativo das caudas. É dado por:

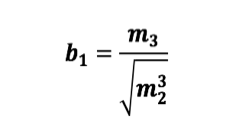
O coeficiente de achatamento dá-nos a ideia sobre uma maior ou menor concentração junto ao centro.Este coeficiente mede o grau de achatamento de uma distribuição, considerado em relação ao da distribuição normal (igual a 3). É dado por: