Funções Periódicas

Uma função,

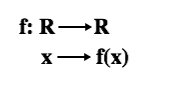
é periódica se e somente se existe um número real positivo k tal que
f(x) = f(x + k)

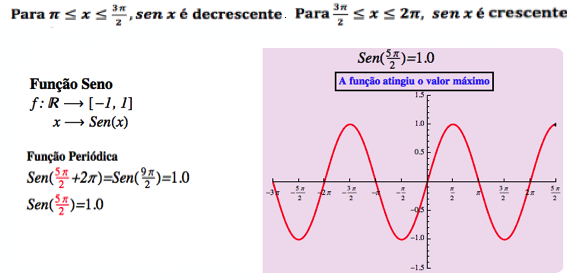
Função Seno

A função Seno é definida por uma aplicação f de R em R do tipo f(x) = Sen(x). É periódica de período 2π uma vez que Sen(x) = Sen (x + 2π). Apresenta as seguintes características:

- Domínio : D(f) = R
- Imagem: Im(f) = [-1,1]
- Período 2π e amplitude 1
- É uma função ímpar já que Sen(-x)= -Sen(x)

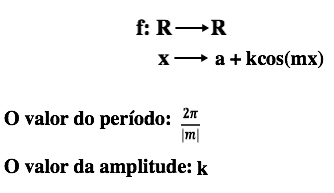
De forma geral, para uma função f definida por:,

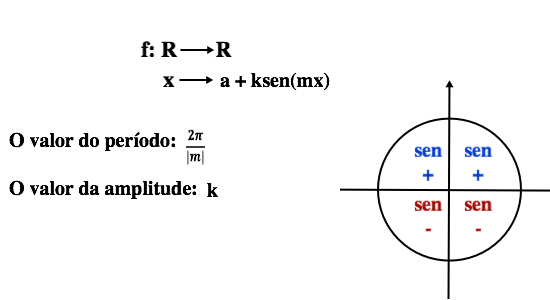
A função seno é positiva para valores entre 0 < x < π e negativa para π < x < 2π,

Função Cosseno

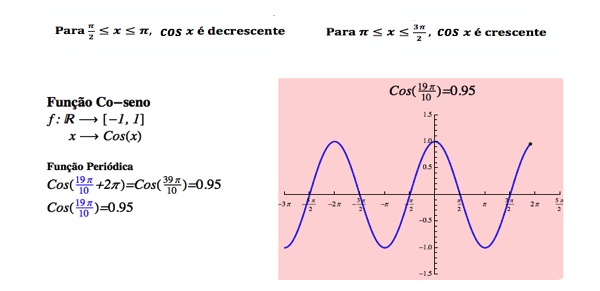
A função Cosseno é definida por uma aplicação f de R em R do tipo f(x) = Cos(x). É periódica de período 2π uma vez que Cos(x) = Cos (x + 2π). Apresenta as seguintes características:

- Domínio: D(f) = R;
- Imagem: Im(f) = [-1,1];
- Período 2π e amplitude 1;
- É uma função par já que Cos(-x)= Cos(x).

De forma geral, para uma função f definida por:,

A função cosseno é positiva para valores entre 0 < x < π/2 e 3π/2 < x < 2π, e negativa para π/2 < x < 3π/2,

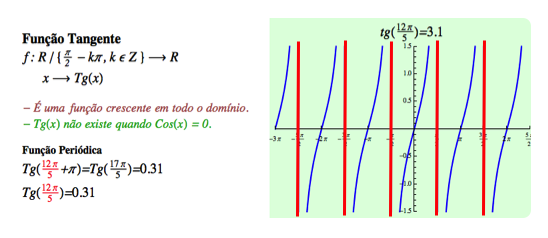
Função Tangente

A função Tangente é definida por uma aplicação f de R em R do tipo f(x) = Tg(x). É periódica de período π uma vez que Tg(x) = Tg (x + π). A função tangente não existe quando Cos(x) = 0 e apresenta as seguintes características:

- Domínio: D(f) = R/ {π/2 - kπ, k ∈ Z };
- Imagem: Im(f) = R;
- Crescente em todos os pontos do domínio;
- É uma função ímpar, pois tg(-x)= -tg(x)

Repare que nos pontos onde cos(x) = 0 a função tangente não está definida.