
Função polinomial do 1º grau
Função polinomial do 1º grau é definida pela aplicação :
f : R → R
x → ax + b
com a ≠ 0 e a, b ∈ R.
A a Lei de formação definida por f(x)=ax + b.
Função polinomial do 1º grau
O coeficiente a determina a inclinação da reta e é chamado de coeficiente angular ou taxa de variação. Analisemos 2 pontos quaisquer da reta:
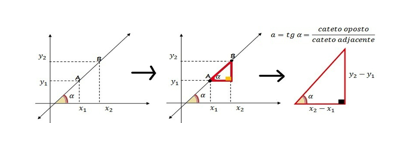
Utilizando o Teorema de Tales, em que duas retas paralelas cortadas por uma transversal formam ângulos correspondentes iguais, deduzimos graficamente que a é definido pela razão:
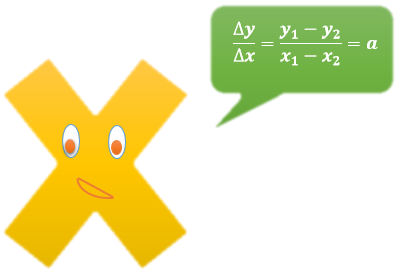

Define-se ainda que:
- Toda função polinomial do 1º grau do tipo f(x) = ax, com a ≠ 0, chama-se função linear.
- Quando a=0 e b ≠ 0 a função do 1º grau recebe o nome de função constante.
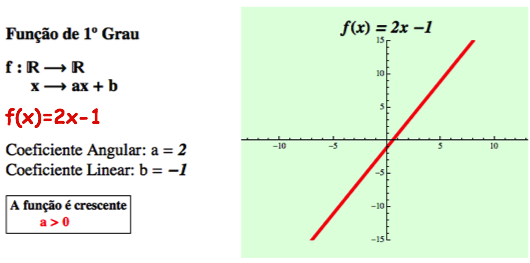
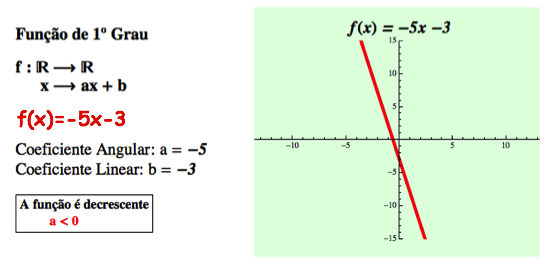
Função polinomial de 2º grau
A função polinomial do 2º grau, também denominada função quadrática, é definida por uma aplicação do tipo:
f : R → R
x → ax2 + bx + c
Com a ≠ 0.

- Na Física envolvendo movimento uniformemente variado, lançamento oblíquo, etc.;
- Na Biologia, estudando o processo de fotossíntese das plantas;
- Na Administração e Contabilidade relacionando as funções custo, receita e lucro;
- Na Engenharia Civil presente nas diversas construções e etc.
As raízes de segundo grau são determinadas da seguinte forma:
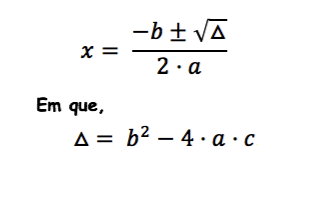
Casos:
Δ > 0 | Δ = 0 | Δ < 0
Δ > 0 : Existem duas raízes reais distintas
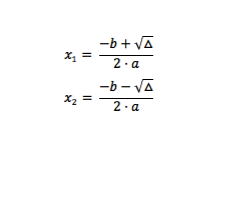
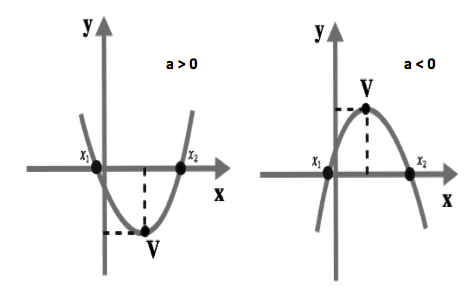
A soma das raízes x1+x2=-(b/a)
O produto das raízes x1x2=c/a

Se Δ = 0 então existem raízes duplas em que x = -b/2a
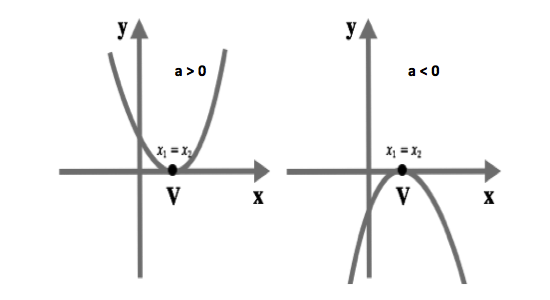
Se Δ < 0 então não existe raiz real.
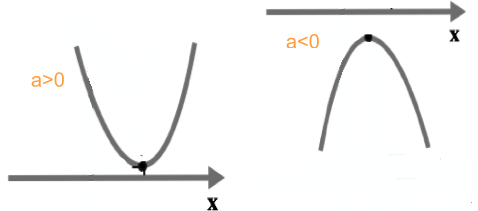
O ponto V apresentado nos gráficos anteriores é o vértice da função do segundo grau e é dado por:
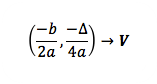
- Para a > 0 V é o mínimo da função.
- Para a < 0 V é o máximo da função.
Exemplo: Considere a função f : R → R em que f(x) = x2 - 4x + 3

Obseve os pontos graficamente:

