Uma dada função f é a associação de elementos de um conjunto A com os elementos de B, cada elemento de A está associado a um único elemento de B.

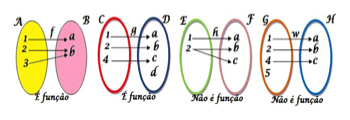
Geralmente, representa-se os elementos de um conjunto por:
- Apresentação: Os elementos estão dentro de duas chaves.
A={a,e,i,o,u}
M={João,Maria,José}

-Descrição: É descrito por uma ou mais propriedades.
A={a: a é uma vogal}
N={x: x é um número natural}

Algebricamente, dados dois conjuntos não vazios A e B, a definição de função é dada por:

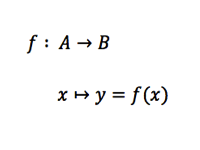
Dizemos que f(x) é a lei de formação da função, sendo o x o elemento de variação.

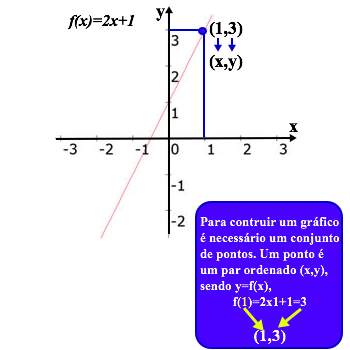
Dado o conjunto A = {-1,0,1}, temos que:

f : A → R
x → 2x + 1

Temos que:

f(-1) = 2 x (-1) + 1 = -1
f(0) = 2 x (0) + 1 = 1
f(1) = 2 x (1) + 1 = 3

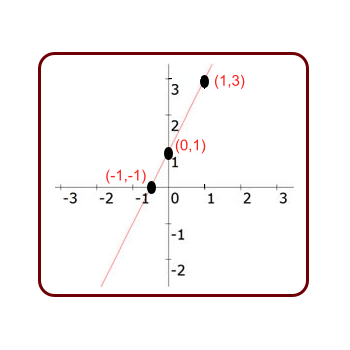
- Conjunto Domínio: é formado pelos possíveis valores que as abscissas podem assumir.

- Conjunto Contradomínio: é formado pelos possíveis valores das ordenadas.

- Conjunto Imagem: é formado pelos valores assumidos pela função dentro do conjunto contradomínio.

- O domínio de f, D(f), é o conjunto de partida, A.

- O contradomínio de f, CD(f), é o conjunto de chegada, R.

- A imagem, Im(f), são os valores assumidos pela função {-1,1,3}.

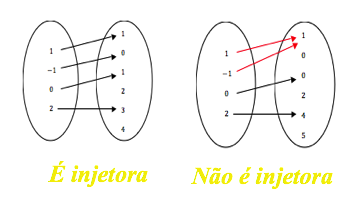
- Uma função será injetora se cada imagem possuir um único elemento correspon- dente ao domínio.

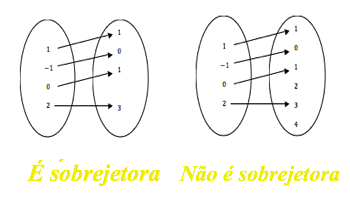
- Uma função será sobrejetora se possuir o conjunto imagem igual ao contradomínio.

Uma função bijetora é simultaneamente injetora e sobrejetora.

Uma função f é crescente num intervalo A do seu domínio D se, e somente se, para quaisquer dois valores diferentes tem-se:

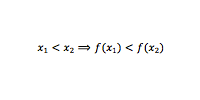
Exemplo : Seja a função real dada por f(x) = 2x+1. Considere x₁ = 1 e x₂ = 2. Substituindo na função dada vem que:

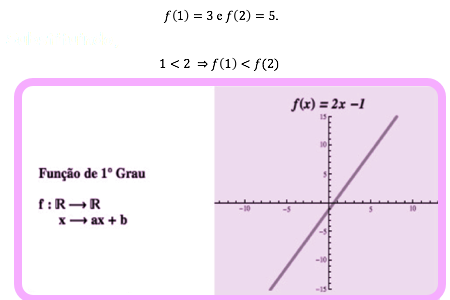
Uma função f é decrescente num intervalo A do seu domínio D se, e somente se, para quaisquer dois valores diferentes tem-se:

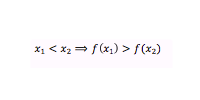
Exemplo : Seja a função real dada por g(x) = -2x+1. Considere x₁ = 1 e x₂ = 2. Substituindo na função dada vem que:

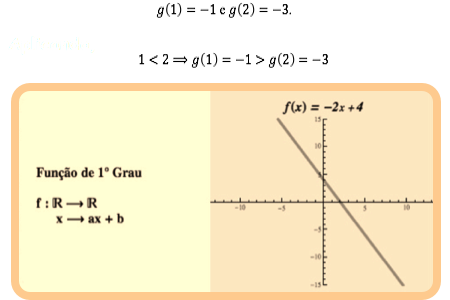
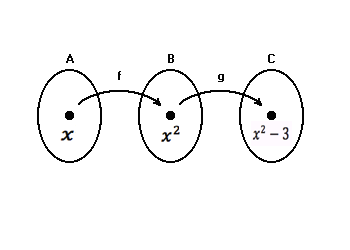
Dadas duas funções f e g, a função composta f∘g (também chamada composição de f e g) é definida por (f∘g)(x)=f(g(x)).

Exemplo: Dadas duas funções f e g, a função composta, também chamada composição de f e g, é definida por

Resolvendo, tem-se:

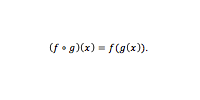
g(f(x)) = g(x²) = x² - 3